Pattern recognition of universal mathematical constants in Acheulean biface formats
Transcraft Consultants, Rua Major F. Hardy 220, Curitiba, Brazil. Email: alcannell@gmail.com
The similar design formats of many Acheulean bifaces has prompted several studies into the use of ‘mental templates’, leading to controversial claims that there may be a relation between length and width equal to the Golden Ratio. To avoid subjectivity, these studies have used aggregate data from assemblages that, by definition, mask the individuality of each tool, its material, any retouching and the original imposed design. Visual pattern recognition is widely used in psychological research and some branches of engineering and a similar technique is presented to highlight the formats of two samples of the Boxgrove assemblage (one random) and examine the presence of universal mathematical constants. A probabilistic analysis suggests that the repeated use of the numbers 2, Pi and Phi and the relationship between them could not have been produced by chance. These relationships appear to be constant over very long time periods and are still used today in modern gemstone design.
Keywords: Acheulean; biface; geometry; format; mathematical constant; aesthetics
A number of researchers have called attention to the apparent constant relation between the length and width of Acheulean bifaces over time and geographical area. McPherron (2000) notes that: “the length and width plot is remarkable for the degree of similarity displayed among handaxe assemblages. What this suggests is that there is an underlying factor that affects handaxe shape in some fundamental way. But the strong association between length and width does not in itself mean that all of these handaxes have the same shape.” Pope et al. (2007) suggest that: “the concept of ‘mental templates’, at least in part guiding reduction strategy, is now an important component of explanations for biface form.” Based on the regression analysis of the measurements made by McPherron (2000), they also state that: “there are compelling results which appear to show a broad agreement between biface shape and the ‘Golden Section’, a ratio controversially claimed to have particularly aesthetic properties.”
Similar observations have been made by Le Tensorer (2006) in which the analysis of several thousand examples of bifaces from the Nadaoiyeh site indicated a preferential length to width ratio of 1.62 – the Golden Ratio (“Le nombre d’or des Grecs correspond a une proportion d’environ 1,62. La mesure de plusiers milliers de bifaces de Nadaoiyeh nous a montré une tendance à la standardisation et la reproduction d’un rapport longuer-larguer preferential assez caractéristique pour chaque faciès. – le nombre d’or”). Gowlett (2011) examined 394 bifaces from Kilombe, 60 from Kariandusi Upper Site (obsidian), 186 from Kariandusi (all from about 1 million years ago) and 103 from the Spanish sites of San Isidro and Pinedo, concluding that: “The evidence suggests a more complex picture: that there was a general and very widespread tendency for hand-axes to be made with breadth/length proportions having a mean value of about 0.61, but also that this central tendency emerges from a swarm of other values; that the allometry factor has the consequence that far broader and far narrower bifaces were regularly made; and, in some biface sets, other proportions tending towards 0.50 were actively preferred so strongly that the 0.61 value scarcely occurs; and that the value B/L 0.50 seems actively favoured in long bifaces in all sets, as well as occurring commonly in Thickness/Breadth (T/B) relations. In the face of all the variation, there can be no case for arguing a deep or hard-wired imposition of any particular proportion in artifacts, but the data strengthen the idea that there is some firmly established human disposition to like particular ratios of shape.” It should be noted that Gowlett uses the Width (Breadth-B) to Length (L) ratio of 0.61 – or phi, rather than the inverse of 1.61 – Phi; similarly the proportion of 0.50 is the inverse of the constant 2.
Regional or epoch differences in biface formats have been estimated using a “polar coordinate technique” (Wynn. & Tierson 1990), but again, the major problem with regression analysis of the dimensions of large samples of bifaces is that individual aesthetic expression is lost in the aggregate values. Each tool had its own history based on the tastes of the maker, the raw material used and any need for final retouching. This taste or template can be understood as a shape emerging from a complex system of operational sequences guided by simple sets of rules, rather than a fixed and projected design. Thus an examination of any underlying biface geometry needs to be based on this individuality of design.
The ‘human eyeball’ method of pattern recognition and visual examination is still used in many modern technologies (such as quality control of electronic components) and although the expression “Pattern Recognition” now has a specific meaning in electronic engineering and computer science (the study of algorithms and methodologies used to automatically extract meaningful patterns from big datasets), in this paper, the term 'Visual Pattern Recognition' is used in the wider sense, such as in the field of psychological research. This topic will be explored in greater depth in a subsequent paper by the author on the possible mechanism of the deep seated attraction to these formats.
The Boxgrove assemblage was chosen for this task as the tools were mostly found ‘in situ’ with minimum ‘rolling’ and are well-known for their meticulous and craftsmanship. With the kind assistance of the British Museum, high quality images of the assemblage were used, as taken by Dr Mathieu Leroyer during 2010 at Franks House, British Museum, with the aid of CNRS team, 'Ethnologie préhistorique' (UMR 7041) and the University, Paris 1 - Panthéon Sorbonne. Dr Leyroyer selected an initial sample of typical formats encountered in the assemblage, but to avoid problems due to the possible “cherry-picking of samples”, in which modern aesthetic tastes determine the tools to be examined, a random sample was also chosen by Dr Leroyer by picking numbers from a hat.
The format to be studied was considered to be two-dimensional (flat) and based on the digitally enhanced outlines using COREL PhotoPaint software. The geometric templates used in manufacture or retouching were determined by retrofitting expressions of Universal Constants onto the digital drawings and allowing the enhanced original shapes to be clearly seen. Particular attention was directed to the format of the butt, the angle of any distinct point formed by straight edges and any curves used on the ‘blades’ forming the point.
An assessment was made to see if this ‘degree of fit’ could be statistically determined using PAST software as in the morphological analysis of bone and stone bifaces from Castel di Guido (Costa 2010), but this option was rejected as this technique ‘masks’ the individuality of each tool and, due to the presence of imperfections or damage on the tools, a visually ‘poor’ fit could offer a better statistical value than an exceptionally ‘good’ fit, if the latter had a partly damaged edge.
To find the best ‘fit’ the outline of the tool was examined to see if the sides were ‘ovate’ or ‘pointed’. Previous experience with images of biface tools and geometric forms had indicated that for ovate tools, the best fit can normally be found by using sections of a Golden Ellipse. The biface ‘butts’ generally conformed to either a circle or a Golden Ellipse. Once the best fit – based on visual pattern recognition - had been established, the relationship of the geometric figures to each other was examined. The presentation allows for individual subjective judgment of these ‘best fits’ and binomial probabilistic analysis examined the probability that the relationships between the geometric figures could be randomly generated.
The expressions of Universal Constants examined were:
• 2 (and the inverse relationship ½);
• Pi – circles and sections of circles
• Phi – expressed as the ratio of Length/Width (L/W), sections of the Golden Ellipse and the angles of 18 and 36 degrees. [An ellipse is a curve on a plane such that the sum of the distances to the two focal points is constant for every point. Ellipses have two mutually perpendicular axes about which the ellipse is symmetric; the larger one is the major axis (LE), whereas the smaller is the minor axis (WE). A Golden Ellipse is one where the ratio between the major and minor axis is equal to Phi. Phi is the unique number in which Phi2 = Phi+1 and can also be expressed as a relation between the numbers 5, 2 and 1, as Phi = (1+√5)/2 and as the sine and cosine of the angles of 18 and 36 degrees, Phi =1+2sin 18o or =1/(2sin 18o), and Phi = 2cos36o.]
Each specimen is presented with an enhanced outline and the suggested geometry superimposed in semi-transparent red and grey. A short explanation accompanies each figure as a guide. The original scale (with each square being 1 cm) has been left in order to show the dimension of each tool.
This is a large biface and a very common format. The butt corresponds closely to a circle with both ‘blades’ of the point using the same section of a Golden Ellipse. The diameter of the circle (D) is close to half the length of the ellipse (LE) so that D=LE/2, (LE/D=2.1 to one decimal place). The tangent where the ellipse touches the circle is thus before the midpoint so that the maximum width of the tool is slightly wider than D. The L/W ratio is just under Phi (the point is damaged so the original full length is unknown). See Figure 1.

Figure 1. Specimen BD 8474.
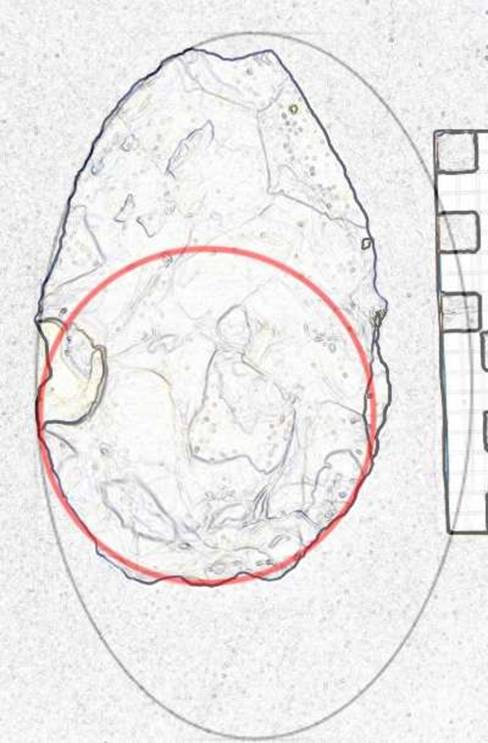
In this medium sized biface, both butt and blades form a single continuum in Golden Ellipse format, L/W is thus Phi. See Figure 2.
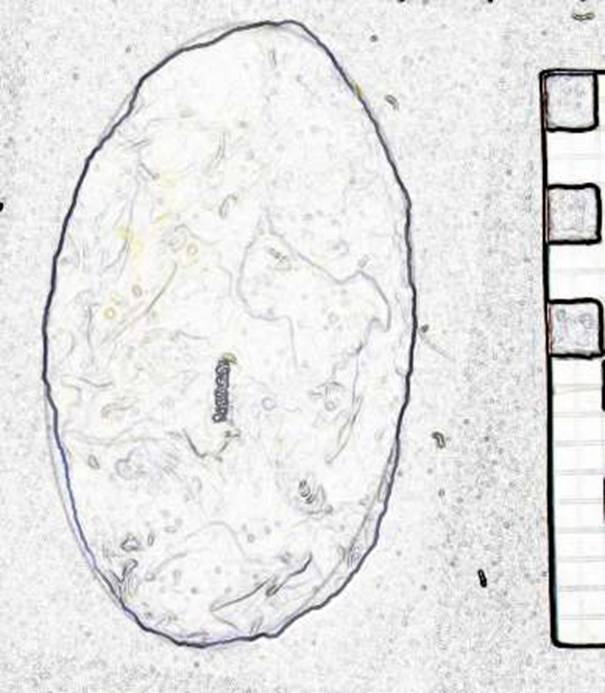
Figure 2. Specimen BD 13576-137.
This large biface has an almost perfectly circular butt, with both blades at a tangent forming the characteristic pointed angle of 36 degrees. Both tangents lie on the same arc from the bisecting line of the blades. The broken point does not allow an L/W measurement to be made. See Figure 3.
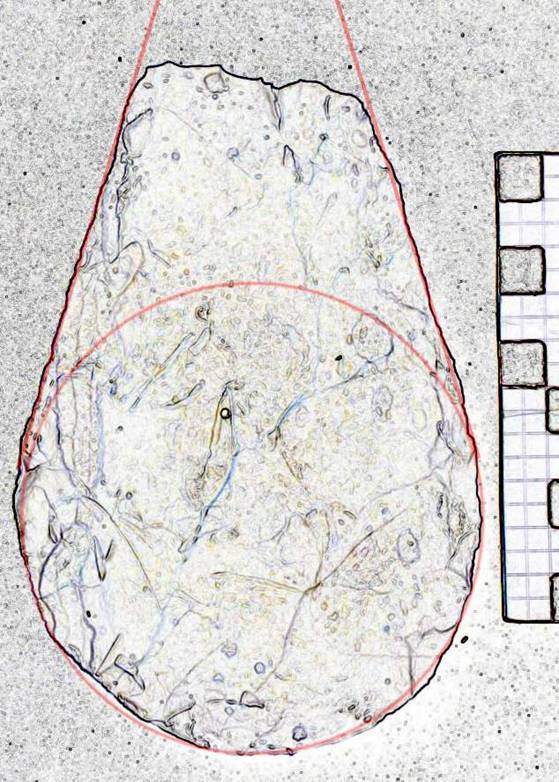
Figure 3. Specimen 317B.
Despite symmetry being recognized as an essential feature of Acheulean bifaces, many examples are unsymmetrical as a result of flaws in the raw material, breakage during knapping or through retouching. Elements of basic geometry in this case are retained: the butt is in Golden Ellipse format with sections of the same ellipse incorporated into the blades. L/W=1.6. See Figure 4.
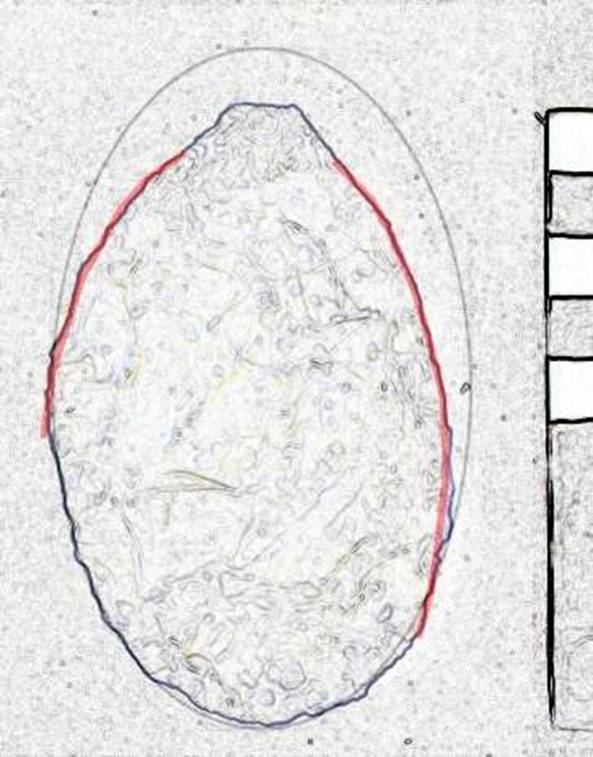
Figure 4. Specimen 31310-31B.
This small tool has a circular butt and blades formed by sections of a Golden Ellipse, in which D is close to LE/2 (LE/D=1.9) The short sections used give a value of L/W=1.38. See Figure 5.
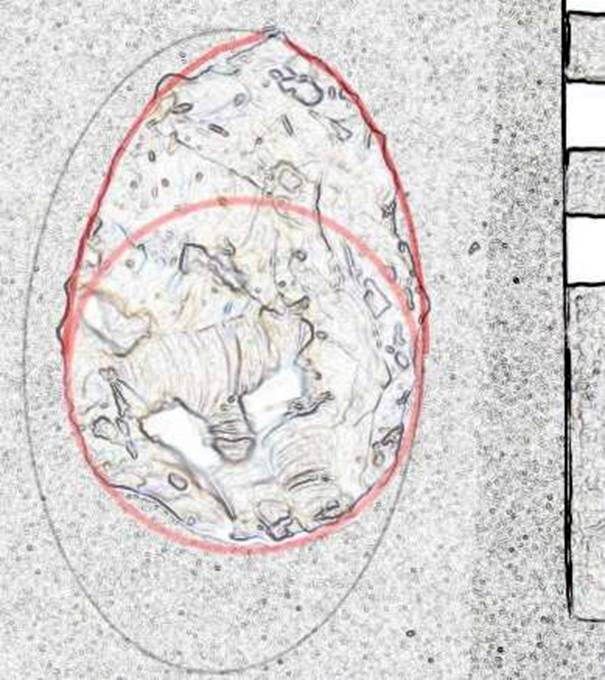
Figure 5. Specimen 31564-33.
This large biface is one of the iconic specimens from the assemblage as the patina and excellence of manufacture give the tool a gemstone-like quality. The butt is circular with Golden Ellipse blade sections, where LE/D=2.1 (or close to D=LE/2). L/W=1.61. See Figure 6.
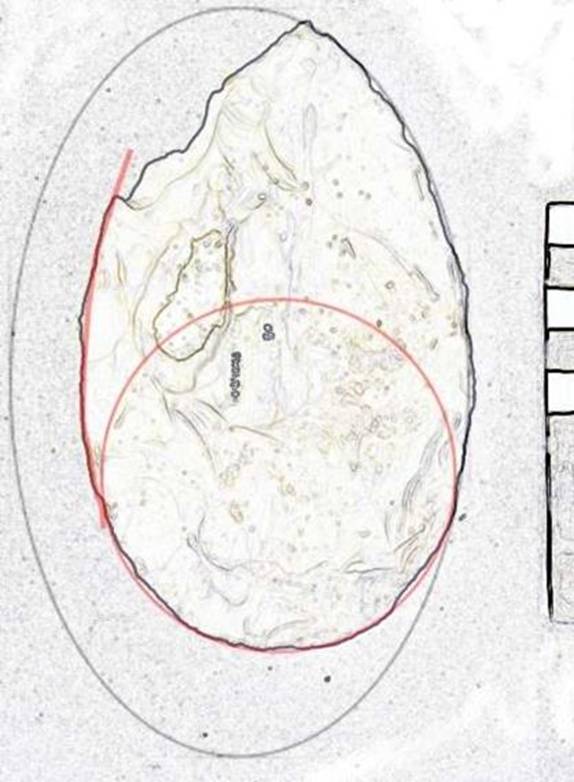
Figure 6. Specimen 12043-50B.
This large and elongated biface has a flawed, damaged or retouched right side. The butt is circular and the long blade is a section of a Golden Ellipse, in this case with the diameter close to the width of the ellipse divided by two (WE/D=1.9). See Figure 7.
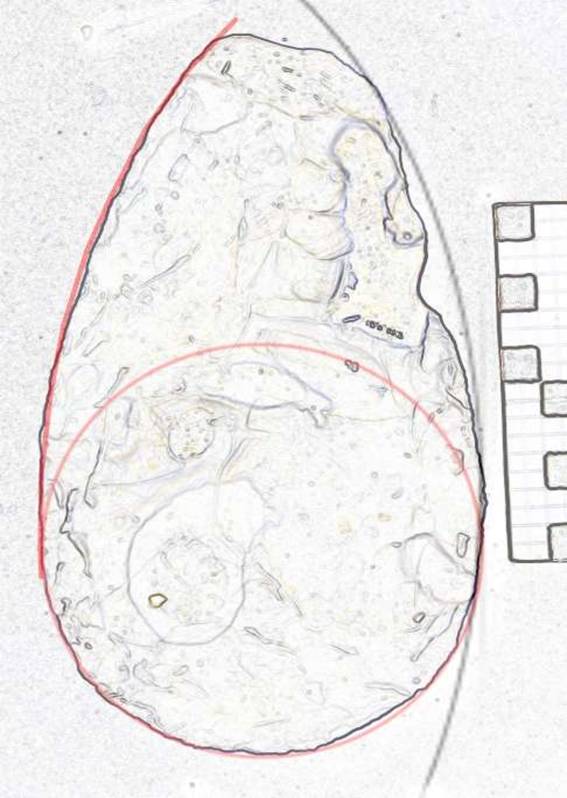
Figure 7. Specimen BD 7812 98.
Dr Leroyer then randomly selected a sample of 14 bifaces from his collection of images. Of these, he suggested removing artifact 136 as this appears to be a discoid core and not a classic ‘handaxe’, (because of the non-elongated shape without differentiation between a point and a butt and absence of soft hammer percussion and final trimming). It was also suggested that artifact 46 not be considered, as this was taken to be a rough-out (absence of final trimming). Artifact 15 also exhibited similar problems and was excluded by the author, as was Artifact 263 - an irregular and small tool with no discernible geometry.
This is a broken or retouched biface with butt in Golden Ellipse. See Figure 8.
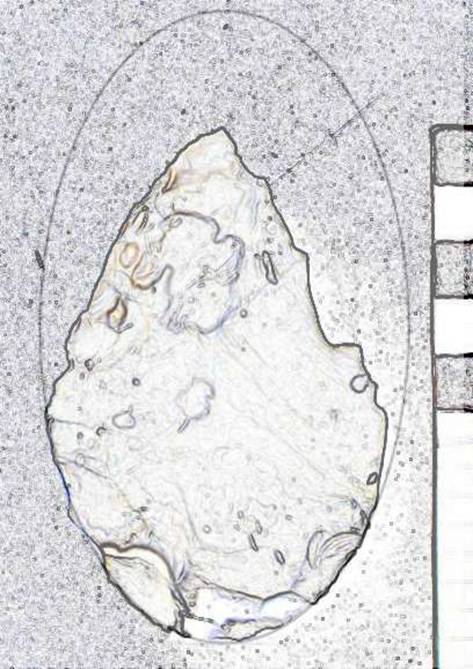
Figure 8. Specimen BO 9480-335.
This is a small biface with LE/D=1.9 and L/W=1.44. See Figure 9.
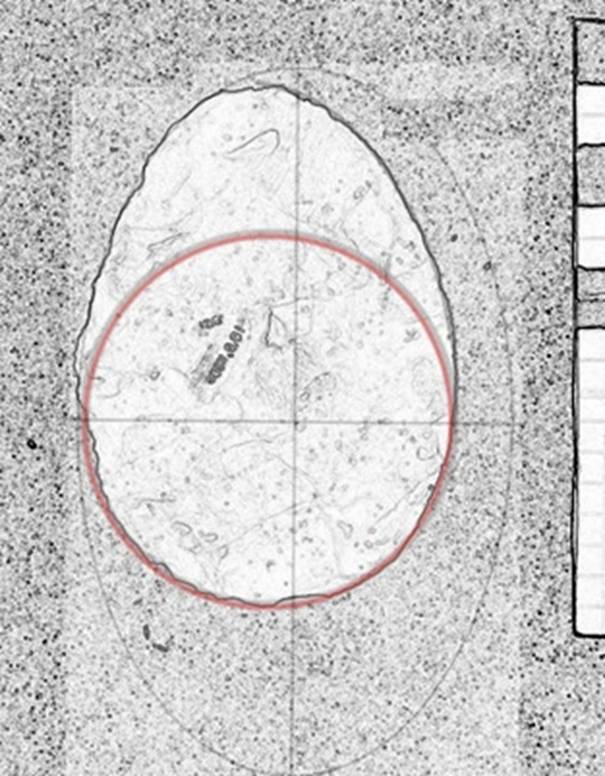
Figure 9. Specimen BD 11080-122.
This is a large biface with a Golden Ellipse format and apparently broken point. See Figure 10.
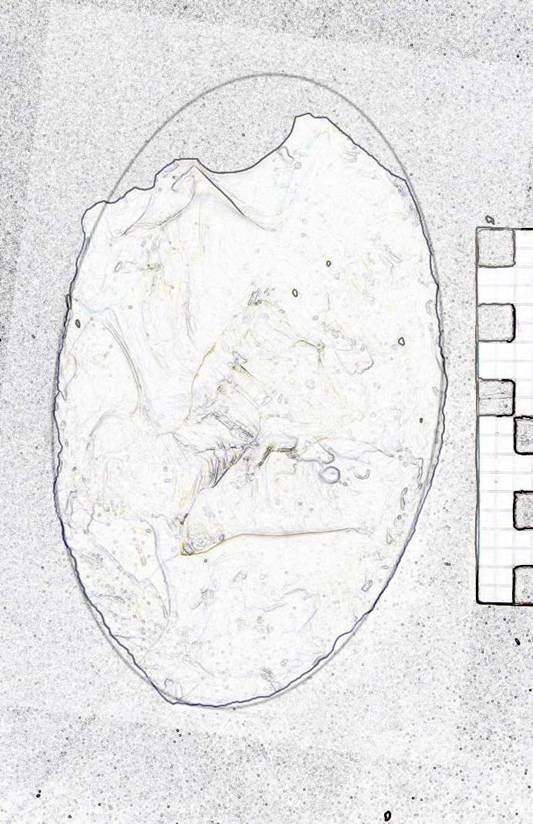
Figure 10. Specimen BD 12418-128.
This biface has an unsymmetrical point. The butt is a section of a Golden Ellipse and both sides of the point use a section of another ellipse, the ratio between these ellipses (LE2/LE1) is 1.36. L/W=1.67. See Figure 11.
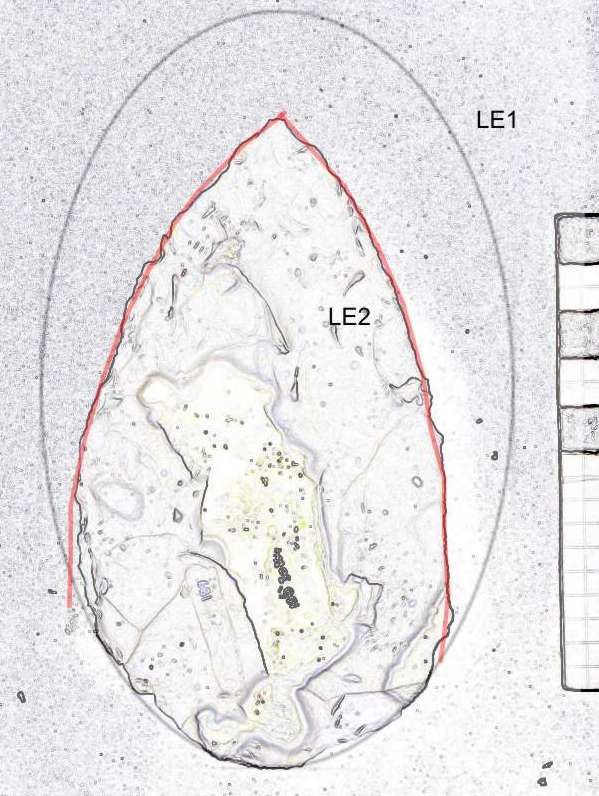
Figure 11. Specimen BD 30864-189.
The butt of this medium sized biface is a Golden Ellipse (1) with the right blade in a section of another Golden Ellipse (2), where LE1/LE2 = Phi/2. L/W=1.54. During manufacture a large flake appears to have been removed from the point area which may have determined how the shape developed. See Figure 12.
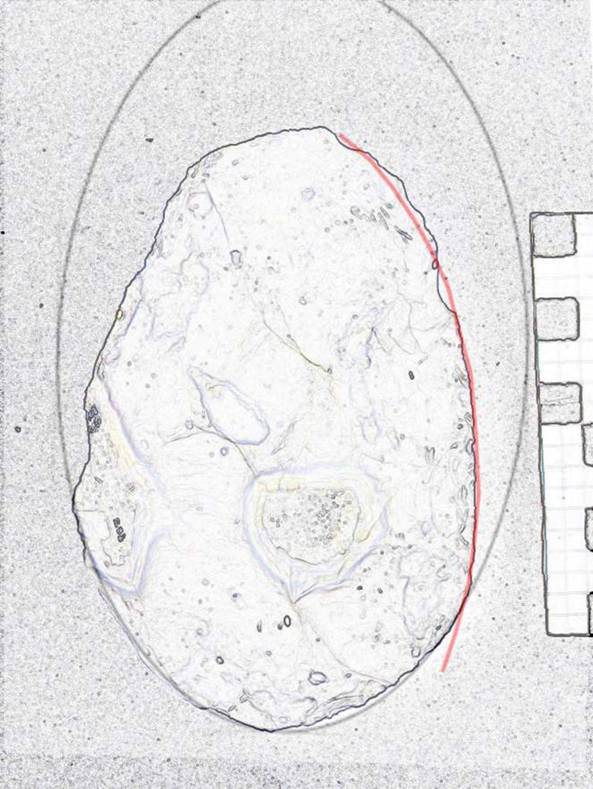
Figure 12. Specimen 1951-253.
This large axe has L/W=1.55, the butt is circular (with a damaged or flawed section) and the blades set at 36 degrees. The left side has a short ‘transition curve’ between the straight and circular sections to allow for a visually smooth effect. See Figure 13.
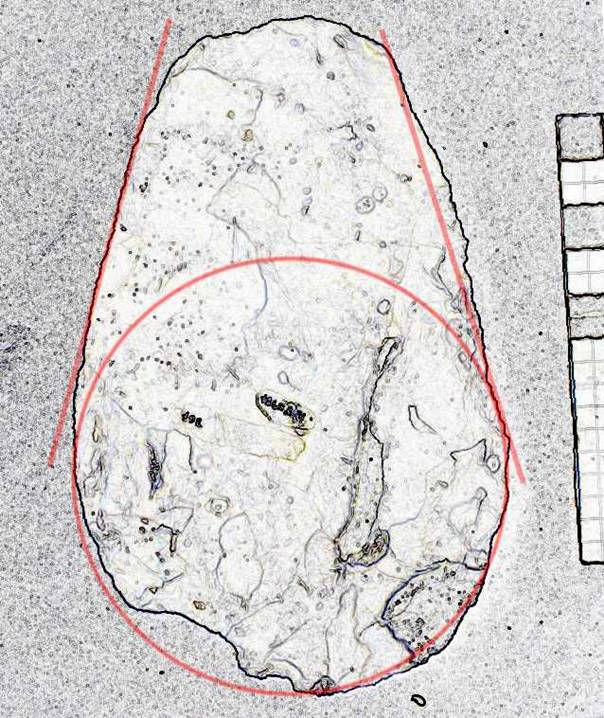
Figure 13. Specimen 11984 367.
The butt is formed by a near perfect circle with the blades in a Golden Ellipse at the widest point and where WE/D=2 and L/W=1.6. Although the point appears to have been sharpened, the unsymmetrical nature suggests that this may have been retouched. See Figure 14.
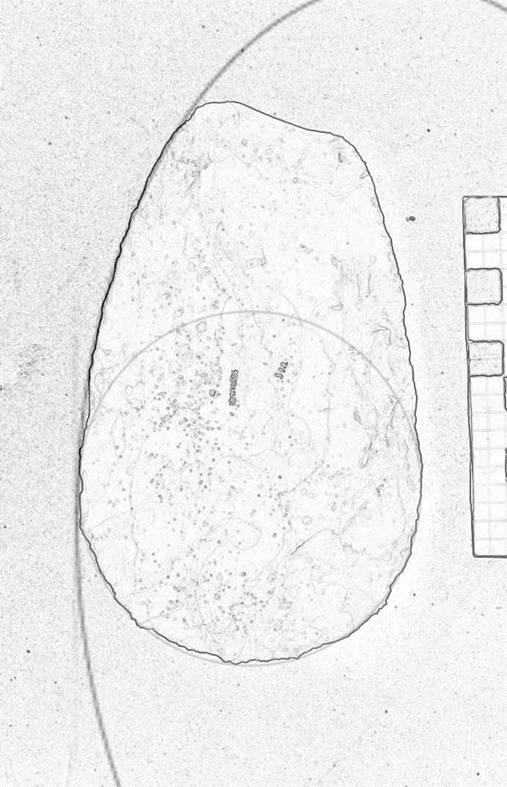
Figure 14. Specimen 12556-372.
The craftsmanship of this tool is not as high a standard as in other bifaces, however, the butt can be seen to be circular with the blades in a Golden Ellipse with a tangent before the maximum width. This same ellipse forms the ‘point’ and although L/W is 1.5, the ratio LE/D is 1.61. See Figure 15.
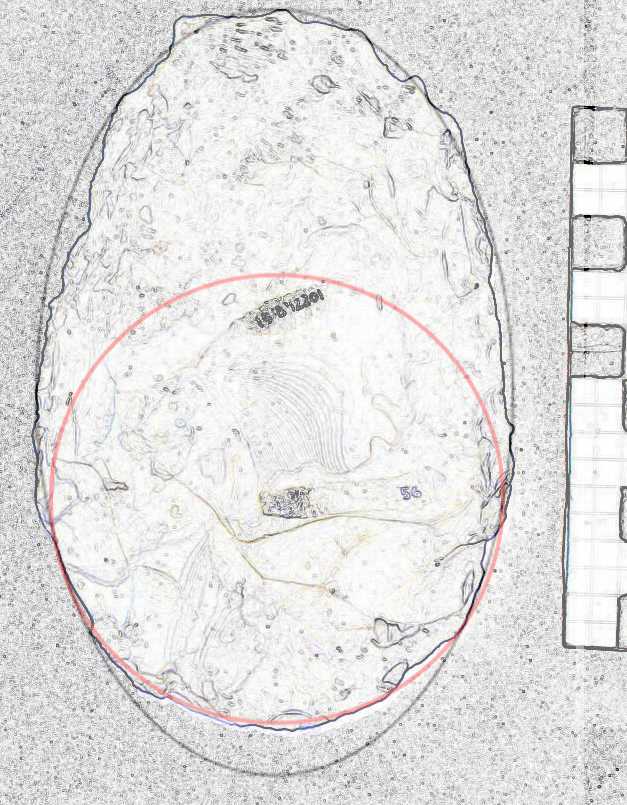
Figure 15. Specimen 12201-56.
This small biface has circular butt with the right blade as a section of a Golden Ellipse where LE/D=2.1. The point appears to be damaged and un-retouched in the original image, L/W=1.55. See Figure 16.
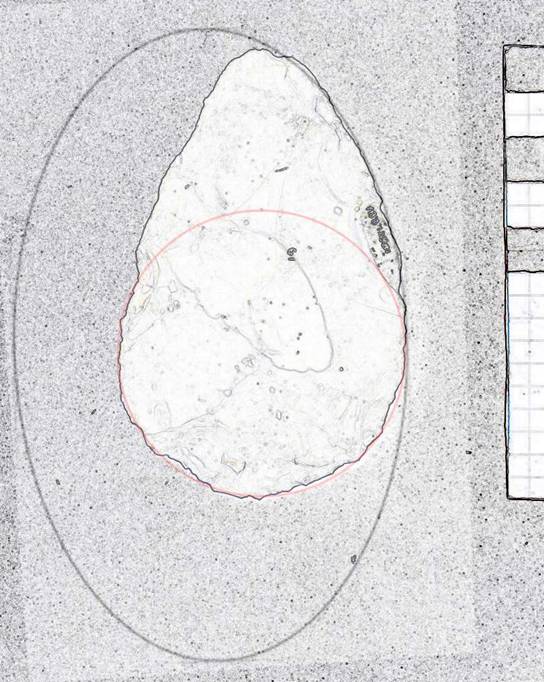
Figure 16. Specimen 12881-61.
Table 1 presents a summary of the expressions recognized (noted in grey). Of the 16 specimens that allow an estimation of L/W, only 6 are close to the value of Phi: the average value of the samples being 1.57. Several bifaces are clearly longer and some of the smaller examples have values that cluster around 1.5 or 1.38. An initial result would thus be that the sceptics are right – there is no Phi based L/W universal template that necessarily determines biface design.
However, both samples show similar levels of geometric expression of the numbers 2, Pi and Phi. Modern notions of ‘attractiveness’ apparently do not create a cherry-picking of samples and this is in itself a strong indication that our modern tastes, in terms of what we find interesting or attractive, are deep rooted in archaic populations.
Of the 16 specimens that were effectively analysed in terms of geometric design, all had expressions of Phi: in the format of the butt, in overall plan and – most frequently - in forming the blades or points as sections of a Golden Ellipse or in a 36 degree angle.
Table 1. Summary of the mathematical expressions and computed relationships in samples of the Boxgrove assemblage.
|
Expressions of Constants |
||||||
|
Pi |
Phi |
|||||
|
Item |
Initial Sample |
Circle |
Golden Ellipse |
36° angle |
Relation of D to ellipse |
L/W |
|
0 |
BO 9868 - 336 |
RTP |
1.61 |
|||
|
1 |
BD 8474 - 110 |
LE/D=2.1 |
1.59 |
|||
|
2 |
BD 13576 - 137 |
1.62 |
||||
|
3 |
317 B |
|||||
|
4 |
31310 - 31 B |
1.60 |
||||
|
5 |
31564 - 33 |
LE/D=1.9 |
1.38 |
|||
|
6 |
12043 - 50 B |
LE/D=2.1 |
1.61 |
|||
|
7 |
BD 7812 - 98 |
WE/D=1.9 |
1.72 |
|||
|
Random Sample |
Pi |
Phi |
||||
|
8 |
B0 9480 - 335 |
LE2/LE1=1.62 |
1.5 |
|||
|
9 |
BD 11080 - 122 |
LE/D=1.9 |
1.44 |
|||
|
10 |
BD 12418-128 |
1.6 (broken) |
||||
|
11 |
BD 30864 - 189 |
LE2/LE1 = 1.36 |
1.67 |
|||
|
12 |
1951 - 253 |
LE1/LE2= Phi/2 |
1.54 |
|||
|
13 |
11984 - 367 |
1.55 |
||||
|
14 |
12556 - 372 |
WE/D=2.0 |
1.6 |
|||
|
15 |
12201 - 56 |
LE/D=1.61 |
1.5 |
|||
|
16 |
12881 - 61 |
LE/D=2.1 |
1.55 (broken) |
|||
Notes. The shaded area represents the presence of an expression of the given constant. Abbreviations. L = Length of the artefact (its major dimension); W = Width of the artefact (its maximum dimension at right angle to Length); D = Diameter of any circle that best conforms to the tool format – normally the butt; LE = Length of the Golden Ellipse that best conforms to part of the tool format – normally the point or blades; WE = Width of the Golden Ellipse that best conforms to part of the tool on its minor axis; and RTP = resolution too poor for analysis.
Ten specimens had circular butts, some of exquisite craftsmanship, and even the most hardened sceptic would find it difficult to acknowledge that they were designed to be circular in shape.
Once the geometric elements had been adjusted to the best ‘fit’, their dimensions were examined, in particular the length and width of ellipses (LE and WE) and the diameter, D, of any circle. Repeatedly, the ellipses and diameters were found to possess an internal relationship, the most common being the diameter of the circle used (butt) being approximately half the length of the ellipse used for the blades (D=LE/2), which appears five times (items 1, 5, 6, 9,and 16). The use of the width of the ellipse (D=WE/2) is present in two cases (7 and 14) and more complex ratios between the diameter and ellipses three times (11, 12 and 15).
As both of the samples contained similar geometrical elements, the specimens have been considered as a single sample for analysis. The constant Pi is expressed as sections of circles. Although it is possible that the butt of a single specimen could have been made by chance in the form of a section of a rough circle, the probability that 10 out of 16 specimens could have been made with the same format, however, tends to zero – especially when considering the quality of many designs. The use of the circle can thus be taken as a deliberate and common template.
The second issue concerns the use of Phi in the form of the Golden Ellipse. This ellipse appears in 14 specimens and, in the cases of BD 13576-137 and BD 12418-128, the entire tool is based on a Golden Ellipse. Also of note is that the only tools that do not present butts based on the circle use a Golden Ellipse format: 31310-31B, BO 9480-335, BD 30864-189 and 1951-293. The probability of this choice being the result of chance again tends to zero.
The probability of the relation D to LE and WE being random can be computed by considering that the length of an ellipse (LE) used to form practical blades could be a value of D to about 4D as shown in Figure 17 below; thus for a value of D of 10cm, this implies a LE range of 10 to 40cm.
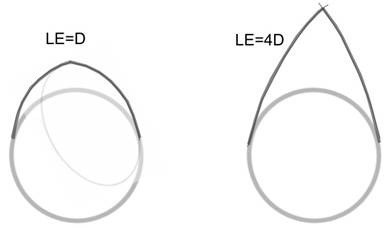
Figure 17. Bifaces formed with points based on LE=D and LE=4D.
For a uniform distribution of values of LE to be within one decimal place for the ratio LE/D=2 (1.9-2.1) implies a tolerance of 1cm above or below the value of 20cm, thus the probability would therefore be 2/(40-10) or 1/15. A binomial distribution appears when a binary random experiment is repeated several times. It computes the probability of obtaining exactly n successes of one event of probability p in N trials. The binomial distribution formula is:
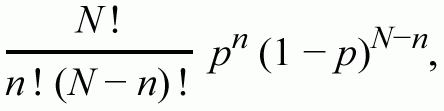
The probability of five specimens having the same value thus in a small sample is a binomial problem that resolves to a value of the order of about two in ten thousand. If the format of WE/D=2 is included in this estimate, then n becomes 7 and the odds of a relationship involving D, LE, WE and 2 being random are less than one in a million. It is therefore very unlikely that these relationships are random.
The angle of 36 degrees is present in only two specimens. The L/W value of 1.36 to 1.38 is found in two specimens. This is often found in modern gem design and biface formats and, although beyond the scope of this present study, it is worth mentioning that this is e/2, where e is Euler’s Constant – the basis of exponential growth and natural logarithms.
Finally, the relationship L/W can also be tested by considering a typical range of values from 1.2 to 2.4 (as typically found in the archaeological record and illustrated in Figure 3.15, Emery 2010) and taking the probability of a specimen having a ratio of 1.6-1.62 as being a uniform chance event, this probability is thus: (1.62-1.6)/(2.4-1.2)=2/12.
The probability of 6 samples in 17 trials conforming randomly to this ratio is again a binomial problem and can be resolved to a value of less than 4%. Hence, although not necessarily a template for all biface designs, there is a very high probability that many L/W values will be within this range and that this clustering around Phi would be detected in aggregate analysis - as has been found in the previous studies of this relationship.
If the use of the same geometry in biface design has been constant over very long time periods, this is an indication that aesthetic taste has been a part of archaic humanity for a similar period. This hypothesis can be checked by examining lithic design over time. At 65kya, for example, the bifaces found at Lynford Quarry together with a large number of mammoth remains (English Heritage 2012) are removed by an order of magnitude from Boxgrove. In the case of specimen 40416 (Figure 18) the dimensions and format are almost exactly the same as 12043-50B from Boxgrove; the butt is circular and the blade is formed by sections of a Golden Ellipse in which LE/D=2 – a stunning example of how strongly these formats may be hardwired and a possible indication that the tools may have been used for similar purposes. Example 40548 (Figure 19) has a ‘blade’ set at 36 degrees and a butt that is based on a circle.
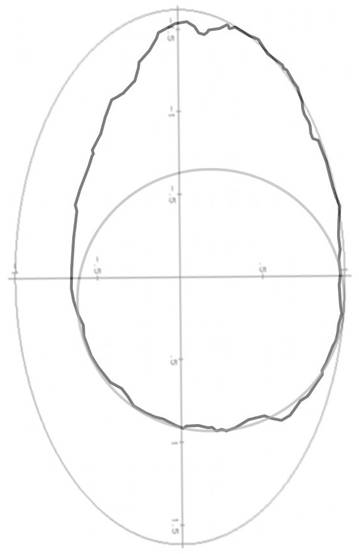
Figure 18. Outline of Specimen 40416, Lynford Quarry (from author’s photograph).
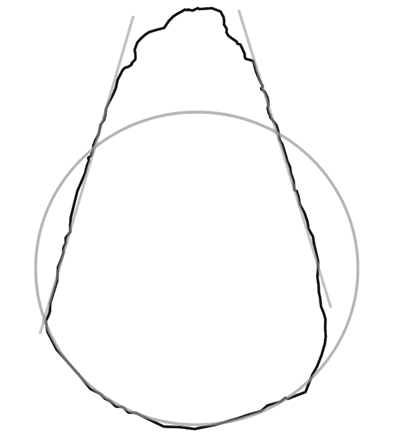
Figure 19. Outline of Specimen 40548 Lynford Quarry (from author’s photograph).
The knapping of bifaces is still carried out in order to understand how these tools were made. The example below in Figure 20 shows a modern “tool” in which the knapper started with a blank with one flat surface and ended with a format based on a golden ellipse, the width of the tool being half the length of the ellipse. When questioned on this, the knapper (a professional paleoanthropologist) mentioned that no specific design was intended – other than the intention to produce a ‘handaxe’ type tool - no mental template was selected and he was unaware that a golden ellipse had been used or that there was a relation between the width and this ellipse.
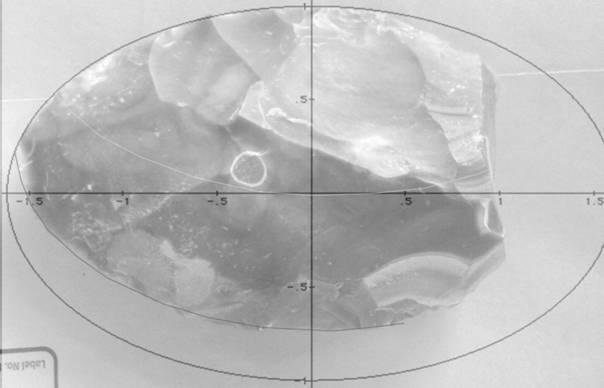
Figure 20. Geometry of a modern biface.
There is one kind of stone artefact which is still being manufactured by highly skilled craftsmen: gemstones. Most gems are made in circular formats; however, according to the Gemological Institute of America (GIA), there are other shapes, termed “fancy”, of which the four main formats are: emerald, pear, marquise, and oval. In 2009 the GIA examined the preferences for length to width ratios for each format. Groups of trade professionals and consumers viewed images and diagrams of unset stones, and were asked to select their preferred design. The surveys indicated that: “particular length-to-width ratios were preferred for each fancy shape with the preference diminishing above or below that ideal. For a Pear Cut both consumers and trade professionals had peak L/W ratio preferences at 1.6. For an Oval Cut both survey groups again preferred ratios around 1.6.” (Blodgett el al. 2011).
It should be pointed out that an Oval Cut is actually an ellipse, thus the preferred shape was essentially a Golden Ellipse. A Pear Cut is based on circles and ellipses and a typical outline for a large stone is shown in Figure 21 superimposed on Boxgrove specimen 12043-50B (scale adjusted so that the diameter of the butt circle for both specimens is the same). A Pear Cut diamond from Botswana (outlined in Figure 21) was sold for 27 million dollars in 2013 and has a L/W ratio of 1.61.
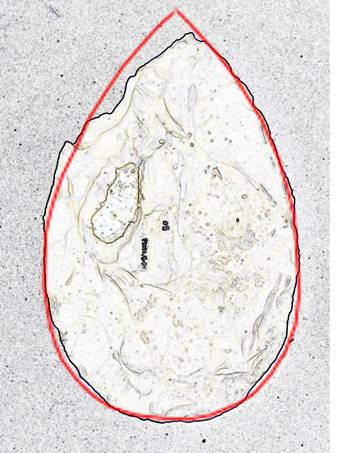
Figure 21. Geometry of pear cut diamond from Botswana superimposed on the outline of Specimen 12043-50B from Boxgrove.
An appreciation of symmetry, the number 2, is found throughout the animal kingdom and symmetry has been found to be present in biface formats in a manner that does not fit a null hypothesis (Lycett 2008) and that cannot be explained as a function of animal butchery (Machin et al. 2007). Expressions of Pi (notated below as π for clarity) can also be seen in the full moon, the setting sun and in the eyes of a nursing mother.
Our attraction to Phi, however, is harder to comprehend. If one of the primary functions of large bifaces was in the penetration of flesh, then a refined serrated stone point formed with one or two elliptical sections is highly efficient. A Clovis point had this format, as do modern steak knives. Form and function thus go together.
Although Phi is normally presented as a ratio between lengths, it is perhaps more important in terms of the transition from one to two dimensions. When a single unit of length is increased by an extra unit in all directions from its mid-point, the area formed is a circle of radius 1 and area of π. When the increase in length from the same mid-point is Phi, the area formed is πPhi2 which is π(Phi+1). Thus as the radius of a circle is increased from 1 to Phi, its area suffers a unit increase of Phi. This is the only number in which linear growth is matched by two-dimensional growth.
For a circle with radius Phi drawn over a circle with a diameter of 1 (radius ½), a line from any point on the former circle that tangents the latter will form the base of a pentagram - the angle of the 5 ‘points’ being 36o. (See Figure 22.)
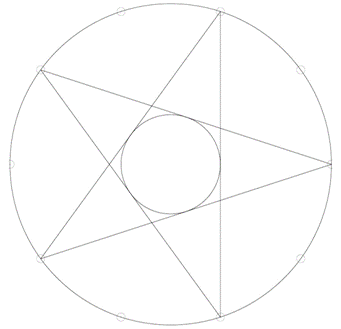
Figure 22. Pentagram based on a circle of radius Phi superimposed on a circle with a diameter of 1.
Humans, like all tetrapods, are pentadactyl with five digits on each limb, thus it is possible that the attraction to expressions of Phi may be related to an appreciation of our own physical structure.
Pattern recognition of individual biface formats allows for a more detailed morphological analysis of the geometry used than regression analysis of whole assemblages or larger data bases. An evaluation of random and selected samples of Boxgrove bifaces strongly suggests that several universal mathematical constants were consistently employed in both samples, specifically the numbers 2, Pi and Phi. The use of circles and sections of a Golden Ellipse was common and in many cases there was also a relationship between the constants such that the diameter of the circle was half the length or width of the ellipse used. Binomial probabilistic analysis indicates that these relationships were not made by chance.
These same universal constants appear in more recent Acheulean bifaces indicating that an attraction for these numbers has been continuous over vast time periods, and their preference in modern gem design for purely aesthetic reasons suggests that modern tastes may have been inherited from archaic populations.
The term “mental template” has been applied to biface design and is highly controversial, especially if taken as a conscious process in which a particular shape is the desired end-product of the bifacial reduction sequence. If, on the other hand, this mental template is considered to be an attraction to a simple set of mathematical constants, any final product will end up as an unconscious expression of these numbers (as in the example of the modern knapper and in the diamond industry). This is similar to the concept raised by McNabb (2004) in relation to the formats of British bifaces: “Rather than being a tightly conceived and culturally sanctioned outline form acquired and maintained through social learning, the shape of a large cutting tool was a variable idea in the mind of the knapper”.
Much of the recent discussion on ‘handaxe’ formats has revolved around the shape of the ‘points’ chosen by the knapper: ovate or pointed. These can be briefly summarized as: the concept of resharpening, in which a ‘basic’ pointed format resolves into ovate as retouching takes place (McPherron, 1995); and raw material constraints, in which ovates emerge as the preferred form (White 1998). This question was studied in depth by Emery (2010) who concludes that: “it seems likely that the reduction hypothesis cannot be used to explain the point/ovate patterning in the British dataset.” As this paper shows, both ‘ovate’ (elliptical) and pointed formats (when in 36 degrees) can be seen as expressions of the same constant – Phi, the choice of either type of point thus being the result of the individual attraction of the knapper to a specific form, the constraints of the material being used and engineering considerations related to usage.
Expressions of this attraction are seen in bifaces from 1 million years ago, through the Boxgrove samples from some 500 thousand years ago to the Neanderthal specimens from Lyford Quarry from 65 thousand years ago, and the same constants are still used today in gem design. This suggests that this attraction could be considered to be “hard-wired” and possibly related to a neurological mechanism that is even older.
Certain tools are said to: “have artistic creativity” (Letensorer 2006), “show a high degree of craftsmanship i.e., they are “well made” (Iovita & McPherron 2011), appear to be ‘over-engineered” (Mithen 2005) or in the case of the giant Cuxton ficron, “be of exquisite workmanship, almost flamboyant” (Wenban-Smith 2004). These qualities are all highly subjective and although it is clear that any appreciation or analysis of format requires that the tool being studied present a well worked shape; at present the study of lithics does not have a standard or guidelines on what constitutes craftsmanship. Rough gemstones are improved in terms of symmetry, shape and reflectivity by the cutting and polishing of facets; a definition of the time and effort involved in biface manufacture could perhaps be expressed in similar terms as the number of ‘facets’ or visible flake removals, allowing different assemblages to be compared according to their level of craftsmanship. The giant Cuxton ficron, for example, was found in the same context as other “roughly made” ficrons and bifaces yet was deemed to be markedly superior in workmanship, Wenban-Smith (2004) noting that: “both sides are straight and perfectly symmetrical”. It is worth adding that these sides form an angle of 18 degrees – once again, an expression of Phi.
Lycett & von Cramon-Taubadel (2008) propose the hypothesis that: “Acheulean handaxe technologies evolved in Africa and dispersed with migrating hominin populations into northern and western Eurasia, under the assumptions of an iterative founder effect (repeated bottlenecking) model.” An engineering model of bifaces as hunting tools (Cannell 2014) also suggests that the spread of Acheulean technology closely matches the geographic spread of Paleoloxodon Antiquus, thus the high quality of craftsmanship – or over-engineering - of many bifaces could be seen as ‘totemic’, a token of respect or an effort intended to “attract” the desired proboscidean prey. It remains to be seen if mathematical constants were used in all regions and whether differences in expressions of these numbers are regionally different and if they show a similar dispersal pattern.
Blodgett, T.A., Gilbertson, A., Geurts, R. & Goedert, B. 2011, Preferred Length-to-Width Ratios Among Fancy Shape Diamonds. Gems & Gemology; Proceedings of the Fifth International Gemological Symposium, 47(Summer): 129.
Boismier, W.A., Gamble, C. & Coward, F.S., (Eds.) 2012, Neanderthals among mammoths : excavations at Lynford Quarry, Norfolk. English Heritage, Swindon, 529 p.
Cannell, A.E. 2014, Proboscidean resources and the engineering of Acheulean lithic technology. Lithic Technology, 39(1): 39-45. doi:10.1179/0197726113Z.00000000031
Costa, A.G. 2010, A Geometric Morphometric Assessment of Plan Shape in Bone and Stone Acheulean Bifaces from the Middle Pleistocene Site of Castel di Guido, Latium, Italy. In: New Perspectives on Old Stones : Analytical Approaches to Paleolithic Technologies (Lycett, S.J. & Chauhan, P., Eds.), Springer New York, New York, NY: p. 23-41. (in English) doi:10.1007/978-1-4419-6861-6_2
Emery, K. 2010, A re-examination of variability in handaxe form in the British Palaeolithic. Doctoral thesis no. 19299 at the Institute of Archaeology, University College London, London, 388 p. URL: http://discovery.ucl.ac.uk/19299/
Gowlett, J.A.J. 2011, Special Issue: Innovation and the Evolution of Human Behavior The Vital Sense of Proportion: Transformation, Golden Section, and 1: 2 Preference in Acheulean Bifaces. PaleoAnthropology (Special Issue: Innovation and the Evolution of Human Behavior), 174. doi:10.4207/pa.2011.art51
Iovita, R. & McPherron, S.P. 2011, The handaxe reloaded: A morphometric reassessment of Acheulian and Middle Paleolithic handaxes. Journal of Human Evolution, 61(1): 61-74. doi:10.1016/j.jhevol.2011.02.007
Lycett, S.J. 2008, Acheulean variation and selection: does handaxe symmetry fit neutral expectations? Journal of Archaeological Science, 35(9): 2640-2648. doi:10.1016/j.jas.2008.05.002
Lycett, S.J. & von Cramon-Taubadel, N. 2008, Acheulean variability and hominin dispersals: a model-bound approach. Journal of Archaeological Science, 35(3): 553-562. doi:10.1016/j.jas.2007.05.003
Machin, A.J., Hosfield, R.T. & Mithen, S.J. 2007, Why are some handaxes symmetrical? Testing the influence of handaxe morphology on butchery effectiveness. Journal of Archaeological Science, 34(6): 883-893. doi:10.1016/j.jas.2006.09.008
McNabb, J., Binyon, F. & Hazelwood, L. 2004, The Large Cutting Tools from the South African Acheulean and the Question of Social Traditions. Current Anthropology, 45(5): 653-677. doi:10.1086/423973
McPherron, S.P. 2000, Handaxes as a Measure of the Mental Capabilities of Early Hominids. Journal of Archaeological Science, 27(8): 655-663. doi:10.1006/jasc.1999.0467
Mithen, S.J. 2006, The singing Neanderthals: the origins of music, language, mind, and body. Weidenfeld & Nicolson, London, 374 p.
Pope, M., Russel, K. & Watson, K. 2006, Biface form and structured behaviour in the Acheulean. Lithics, 27: 44-57. URL: http://www.lithics.org/lithics/lithics27.html
Le Tensorer, J.-M. 2006, Les cultures acheuléennes et la question de l'émergence de la pensée symbolique chez Homo erectus à partir des données relatives à la forme symétrique et harmonique des bifaces. Comptes Rendus Palevol, 5(1-2): 127-135. (in French) ("Emergence of symbolic thought in Acheuean biface formats") doi:10.1016/j.crpv.2005.12.003
Wenban-Smith, F. 2004, Handaxe typology and Lower Palaeolithic cultural development: ficrons, cleavers and two giant handaxes from Cuxton. Lithics, 25: 11-21.
White, M.J. 1998, On the Significance of Acheulean Biface Variability in Southern Britain. Proceedings of the Prehistoric Society, 64: 15-44. doi:10.1017/S0079497X00002164
Wynn, T. & Tierson, F. 1990, Regional Comparison of the Shapes of Later Acheulean Handaxes. American Anthropologist, 92(1): 73-84. doi:10.1525/aa.1990.92.1.02a00050